Knight Probability in Chessboard

View on Leetcode

Given an $n \times n$ chessboard, a knight on square $(r, c)$ attempts to make $k$ moves. Each move, the knight chooses one of 8 possible moves uniformly at random (even if the piece would go off the chessboard) and moves there. The knight continues moving until it has made exactly $k$ moves or has moved off the chessboard. Return the probability that the knight remains on the board after it has stopped moving.

Intuition

Suppose initially, that the knight has a weight of 1, and that for each move, the knight splits its weight equally among the 8 possible moves. Then, the problem of finding the probability of the knight staying on the board after $k$ moves is equivalent to finding the sum of the final weights of each square of the board after k moves.

The problem thus boils down to simulating the knight’s moves, and finding the total weight left on the board after $k$ moves. This can be done recursively, using the following base cases and recurrence relation:

\[\begin{align} \text{Pr}(E_{i, j, 0} \ | \ n) &= 1 \\ \text{Pr}(E_{i, j, k} \ |\ n) &= 0 \quad \text{if } i \notin [0, n-1] \text{ or } j \notin [0, n-1] \\ \text{Pr}(E_{i, j, k} \ | \ n) &= \sum_{(a, b) \in D} \text{Pr}\big(E_{i+a, j+b, k-1} \ | \ n\big) \end{align}\]

where $E_{i, j, k}$ is the event that the knight on square $(i, j)$ stays on the board after $k$ moves and $D$ is the set of possible moves.

Complexity

Considering the state space of the problem, there are $n^2$ possible squares that the knight can be on, and $k$ possible moves that the knight can make. Thus, the measure of the state space is $O(n^2k)$. Adopting a bottom-up approach, every state will be updated exactly once. Thus, with an appropriate $O(1)$ update function, we can solve this problem in $O(n^2k)$ time and $O(n^2k)$ space.

However, for any given initial state $(\mathtt{row}, \mathtt{column}, k)$, several of the states are never visited. Hence, a top-down approach with memoization would be more time-efficient (albeit only by a constant factor).

Further Optimization

Using the symmetry of the chessboard, we can reduce the runtime by a factor of $8$, by considering only the states within the first quadrant of the board. This is because squares in the other quadrants are equivalent to their counterparts in the first quadrant, and thus, have the same probability of the knight staying on the board after $k$ moves.

We can visualize this by noticing that by folding the chessboard along the lines denoted in the diagram below, the shaded region of the board is folded onto the unshaded region.

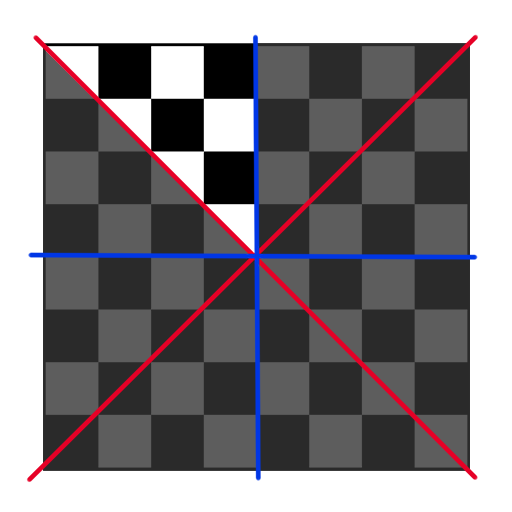
Approach

To implement the above recurrence relation, we will define the following:

• A list D encoding the 8 possible knight moves.
• A function fold(i, j) that returns the coordinates of the square in the first quadrant that $(i, j)$ is equivalent to.
• A recursive function dp(i, j, k) that returns the probability of the knight staying on the board after $k$ moves, starting from square $(i, j)$. This function will be memoized using the @cache decorator from the functools module.

The result of the problem is then given by dp(row, column, k).

Code

class Solution:
    def knightProbability(self, n: int, k: int, row: int, column: int) -> float:
        """Top-down approach with state space reduction"""
        # list of possible knight moves
        D = [(-1, -2), (-1, 2), (1, -2), (1, 2), (-2, -1), (-2, 1), (2, -1), (2, 1)]

        def fold(i, j):
            if i < j: 
                # fold along main diagonal (downward sloping red)
                i, j = j, i

            if i + j > n - 1: 
                # fold along anti diagonal (upward sloping red)
                i, j = n-j-1, n-i-1

            if i > (n-1)//2: 
                # fold along horizontal axis (blue)
                i = n-i-1

            return i, j

        @cache
        def dp(i, j, k):
            if i < 0 or i >= n or j < 0 or j >= n:
                # not on board
                return 0
            if k == 0:
                # no more moves
                return 1
            return sum(dp(*fold(i+a, j+b), k-1) for a, b in D) / 8
        
        return dp(row, column, k)